A Cop and Drunken Robber Game on n-Dimension Infinite Grid Graphs

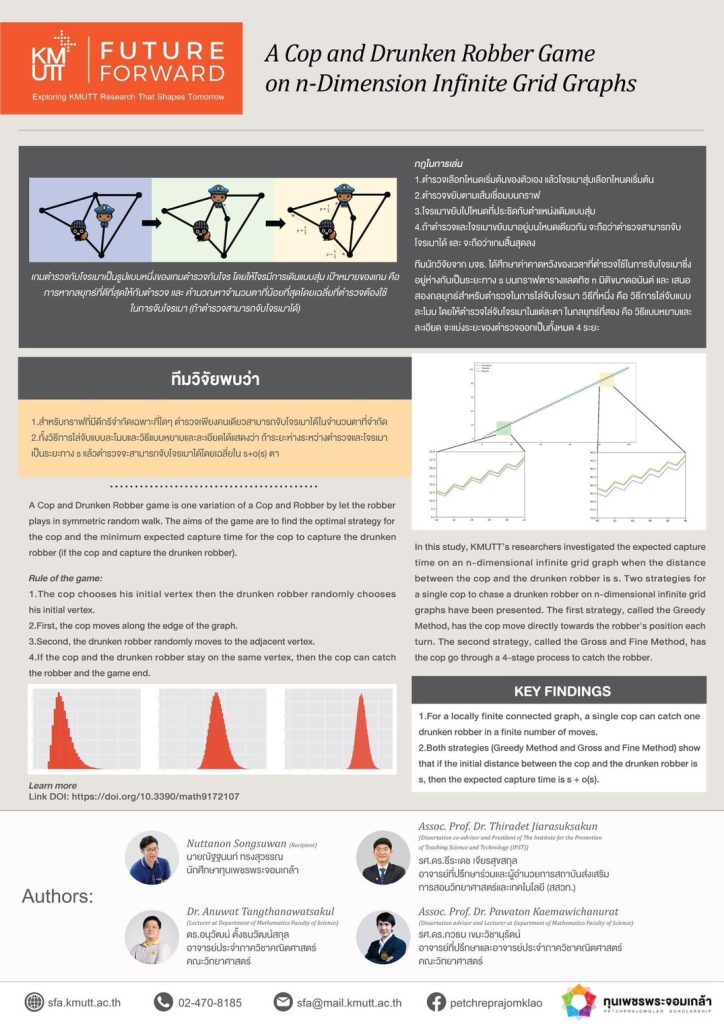
A Cop and Drunken Robber game is one variation of a Cop and Robber by let the robber plays in symmetric random walk. The aims of the game are to find the optimal strategy for the cop and the minimum expected capture time for the cop to capture the drunken robber (if the cop and capture the drunken robber).

𝗥𝘂𝗹𝗲 𝗼𝗳 𝘁𝗵𝗲 𝗴𝗮𝗺𝗲:

• The cop chooses his initial vertex then the drunken robber randomly chooses his initial vertex.
• First, the cop moves along the edge of the graph.
• Second, the drunken robber randomly moves to the adjacent vertex.
• If the cop and the drunken robber stay on the same vertex, then the cop can catch the robber and the game end.

In this study, KMUTT’s researchers investigated the expected capture time on an n-dimensional infinite grid graph when the distance between the cop and the drunken robber is s. Two strategies for a single cop to chase a drunken robber on n-dimensional infinite grid graphs have been presented. The first strategy, called the Greedy Method, has the cop move directly towards the robber’s position each turn. The second strategy, called the Gross and Fine Method, has the cop go through a 4-stage process to catch the robber.

𝗞𝗘𝗬 𝗙𝗶𝗻𝗱𝗶𝗻𝗴𝘀

• For a locally finite connected graph, a single cop can catch one drunken robber in a finite number of moves.
• Both strategies (Greedy Method and Gross and Fine Method) show that if the initial distance between the cop and the drunken robber is s, then the expected capture time is s + o(s).

𝗙𝗨𝗧𝗨𝗥𝗘 𝗙𝗢𝗥𝗪𝗔𝗥𝗗 ❯❯
Exploring KMUTT Research That Shapes Tomorrow